Cognitive Biases are Like Optical Illusions

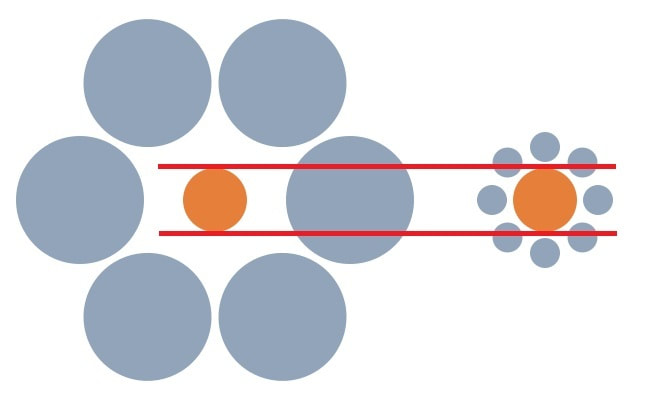
Take a look at this picture:

Which orange circle is bigger? The one of the right? 
Now, look at this next picture:

It clearly shows that both circles are the same size. So, now you know you've made a mistake in your perception. You know that both circles are the same size.
So, when you look back at the first picture you will see the truth about the size of the circles right? Try it.
​
What happened? I'll tell you what happened. You still saw the circle on the right as larger than the one on the left. You can't not see it this way. Even though you now know they are both the same size!

Think about this for a second. You perceive something. You draw a wrong conclusion from your perception. That you made a mistake is clearly shown to you but you still can't see it. This is how optical illusions work.

But, what if it's also how cognitive biases work? In fact, it is. 

Cognitive biases are mistakes we make in our reasoning process when we draw wrong conclusions for a variety of reasons which are illogical. Some of these are related to our particular human psychology. Others are related to our lack of experience with logical inferences. But, all of them can be shown to be wrong and not based on reason and evidence.

The thing is, that once we learn this that knowledge will not automatically allow us to correct these biases. They will still be there and still be as persuasive as ever. 

What we have to do is the same thing we have to do to combat optical illusions. We have to tell ourselves that even though we are seeing things one way, the reality is much different. We have to make a conscious effort to ignore our first intuition and rely on reason and evidence instead. Even if this goes against our most basic intuitions about reality. Does that sound difficult? You bet! Critical thinking does not come naturally!

Let's examine a common cognitive bias through the lens of optical illusions.  Consider this series of numbers:  2, 4, 6.  What rule describes this series?  You can offer examples to test your hypothesis.  If you're like most people you will formulate a hypothesis (for example that the rule is ascending even numbers) and then offer examples to "test" whether your rule is correct.

The problem is all the examples you offer will be attempts to confirm the hypothesis.  But, that isn't really what it means to test your hypothesis.  What you need to do is offer examples that might disconfirm or falsify your hypothesis.  Failure to do this is called the confirmation bias.  

So, for example, suppose you think the rule describing the series is "ascending even numbers."  You can offer an example to confirm this such as "10, 12, 14."  But, if that turns out to be correct that doesn't mean your hypothesis is correct.  There might be another explanation; another rule to fit the series.  

So, let's try another example.  One that might disconfirm your original hypothesis:  "13, 15, 17."  That does fit the rule for the original pattern and it also shows your original hypothesis is wrong.  So, you can discard that and formulate a new hypothesis.  Perhaps your new hypothesis is "ascending by twos."  

Again, you offer examples but again you need to remember to offer examples that might disconfirm your hypothesis.  For example, "1, 2, 3" or even "6, 5, 4."  

Doing this is counter-intuitive but crucial to providing a real test of any hypothesis.  

OK.  So, now you have the explanation of the confirmation bias and a clear example.  Let's test to see whether you can now avoid it.  Check out this website:  www.philosophyexperiments.com/wason/Default.aspx

Let me know how you did in the comments!